Ambi...*looks at paper*..guous Triangle
Ohhhh kaayy..next scribe is me, Francis. I am the next Scribe. I was chosen because I told Justus I would have no internet, until Mar. 15. Mean kid huh.. But guess what! I'm here!
Ambiguous: open to or having several possible meanings or interpretations. (ref. dictionary.com). Basically an ambiguous triangle is a triangle with many different possibilities for side(s) and/or angle(s) measurements, if not already given.
Mrs. Ingram started off by drawing triangles. She drew a scary looking triangle:
Pretty scary ain't it? Well, nothing is missing as though it may look.
For one to solve this triangle, they must use sine law. Find angle B.
.bmp)
SinB = 1.23(since its impossible to have a sine value of >1. Can't find angle B. Therefore it's no triangle!
Now it's time to make another triangle, I promise you, it's much easier.
Now to form 1 triangle. Sine Law comes into play...now.
2.bmp)
SinB = 1 so.. angle B = 90° and Angle A = 60°
Time for the real thing, the real ambiguous triangle.
Angle I: 30° h = 10 i = 6
Since this is ambiguous and it doesn't tell you where the exact position of almost everything. One must algebraically solve it using sine law.
In Quad I H = 56.44°
In Quad II H(2) = 180 - 56.44 = 123.56°
Time to see if we have another triangle in our hands. G = 180 - (30+54.44) = 93.56°
G(2) = 180 - 30(constant value, because it's given) - 123.56 = 26.44° YAY! WE NOW KNOW THERE IS 2 POSSIBLE TRIANGLES!..now it's time to find the measure of side g(use sine law).
g = 11.98 cm(the first g side)
g(2) = 5.34 cm(2nd g side)
We have now found 2 possible triangles. That is an ambiguous triangle folks
We were also given a small assignment to solve an ambiguous triangle without drawing it, but now that we know the equations(look up) we can easily do that! THAT'S THE END! YAY!
The next scriber guy..yes guy, will be! Get ready for HELL! Are ya ready!? ARE YA!? WELL YOU BETTER BE PAUL! THAT'S RIGHT! IT'S PAUL! sorry, I'm so stressed, heh. *wipes sweat off forehead and regain control...*
Solving Trig Functions (for dummies)
Alright, since Nelsa decided to unleash the evil that is scribe unto me, I shall be scribing about the lesson given February 26th, 2007 (For those of you bad people whom may or may not have been there.)Synopsis: The lesson here was comprised mostly of how to solve trigonometric equations (Equations that use Sine, Sosine, or Tangent, in place of x or other variables). We briefly covered the related angles of 30°, 45°, and 60° on the coordinate circle that Cosine, Sine, are derived from, and how those sine, cosine, and tangent measurements can be used to solve triangles/trigonometric equations. We also reviewed the use of CAST, as an effective tool for remembering which trigonometric functions are negative in which quadrants.Table of Contents1.) Coordinate Circle- Sine, Cosine, Tangent Values of 30° , 45° , and 60° - Sine, Cosine, Tangent Values of related angles found in the II, III, and IV quadrants2.) Intro to Trigonometric Equations- Basics- Variations/How to solve them- Finding the Quadrant3.) Conclusion/Afterword to Trigonometric Equations- Notes/Things to remember*Note* Before I get into it, I'd like to mention that if you should find any mistakes with what I've written, feel free to tell me, or change it yourself. I'm not a expert on this and I do make mistakes, so just change it if it's wrong :p Anyways, down the rabbit hole we go, into the world of ridiculous mathmatics*1.) Coordinate CircleWell I'm sure we're all familiar with that lovely circle that the Trig functions, Sine, Cosine, are derived from, the one with the Domain ( -1, 1) and range of (-1, 1). Anyways, in addition to the measures of 30° , and 60° , we found the cosine, sine, and tangent values for 45° which can be seen on the following diagram.Red Background = Quadrant IYellow Background = Quadrant II (Note, I am aware that this is orange, but yellow wouldn't show up on the white background, so don't bug me about it ^.^ )Green Background = Quadrant IIIBlue Background = Quadrant IV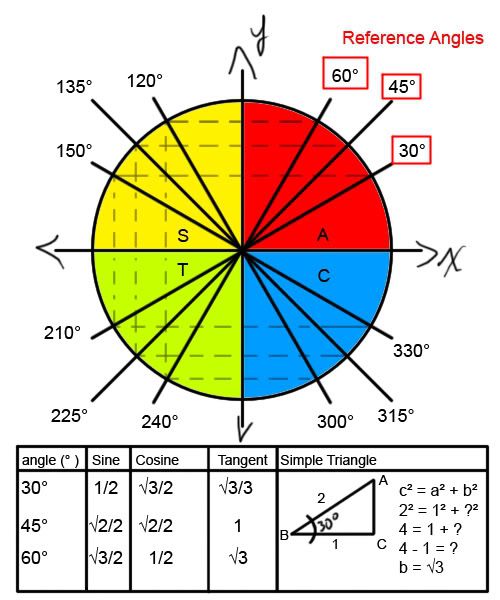
*Note* The triangle in the image is a Right angled triangleNow, you may be wondering, how we found out the values of these angles, at said degrees, and it is with this question in the air, that I introduce you to the simple Right Angled Triangle that our splendid teacher, Mrs. Ingram drew up for us. This triangle has been illustrated on the bottom of the coordinate circle chart I made up. All the math for the simple triangle is included, and should be easy to follow. We started with two sides (The hypotenuse which was 2, and one leg, which was 1.) and using the pythagorean theorum, came up with an exact value of √3 for the final leg. From there determining the values of Sine, Cosine, and Tangent, at each angle (30, 60, and 45 degrees) was simply a matter of using SOH, CAH, TOA. The values of these can be found in the other half of the table where the simple triangle is found. Now finding the values of each related angle in every quadrant was simply a matter of using CAST. *Note* Due to the fact that Sine = y, Cosine = x, and Tangent = y/x quadrant I's sine, cosine, and tangent values are positive. In Quadrant II Sine is positive, while Cosine and Tangent are Negative. In Quadrant III, Tangent is positive (because -sine/-cosine = a positive value), while Sine and Cosine are negative. Finally in Quadrant IV Cosine is positive, while Sine and Tangent values are negative.The values of the remaining angles are as follows.120° ----> Sine = √3/2 Cosine = -1/2 Tangent = - √3135° ----> Sine = √2/2 Cosine = -√2/2 Tangent = -1 } ---- Quadrant II Angles150° ----> Sine = 1/2 Cosine = -√3/2 Tangent = √3/3210° ----> Sine = -1/2 Cosine = -√3/2 Tangent = √3/3225° ----> Sine = -√2/2 Cosine = -√2/2 Tangent = 1 } ---- Quadrant III Angles240° ----> Sine = -√3/2 Cosine = -1/2 Tangent = √3300° ----> Sine = -√3/2 Cosine = 1/2 Tangent = -√3315° ----> Sine = -√2/2 Cosine = √2/2 Tangent = -1 } ---- Quadrant IV Angles330° ----> Sine = -1/2 Cosine = √3/2 Tangent = -√3/3And that sums up this section of the blog (whew ^.^)2.) Intro to Trigonometric EquationsNow that we're past the Coordinate Circle recap, it's time to move onto the main portion of the lesson. Trigonometric Equations. Trig equations aren't much different for any other equation with the exception of the fact that when solving you have to deal with the form:
0 ≤ Θ ≤ 360°To begin we'll look at a generic equationSolve for x2x - 1 = 02x/2 = 1/2x = 1/2To solve this equation is no feat. You simply divide out the coefficient of the variable, and move the -1, over to the other side of the = symbol, inverting the symbol as you go.Now, we're going to apply this to a trigonometric equation.Solve for Θ 2SineΘ - 1 = 0
2SineΘ/2 = 1/2
SineΘ = 1/2
To do this we could follow the exact same procedure, with the exception that at the end of it all, there are a few more steps to do, because of the fact that we're dealing with degrees. So once you've gotten to the final step shown above, you still need to find the value(s) of theta. To do this you simply input the Sine inverse of whatever sine theta equals while positive into your calculator.
Sineֿ¹(1/2) = 30°
Whatever value comes out of this calculation is now your Reference angle, and can be used to find the related angles, thus finishing the question. Because the value of Sine theta was a positive value, you know that the related angle can be, only in Quadrant II (You know this because of CAST. In quadrant II Sine values are positive. You already have the Quadrant I value, which is your Reference angle.) So now the finished equation looks like this.
Solve for Θ
2SineΘ - 1 = 0
2SineΘ/2 = 1/2
SineΘ = 1/2
Θ = 30°
Θ = 180 - 30° = 150°
Now that you've seen the basics of a trig equation, it's time to see the variations you can have.
Solve for Θ
Tan²Θ + 5tanΘ + 6 = 0
Before you start to tackle a question like this you may want to convert it into a more recognizable format.
*Note* If you convert the variable of an equation without stating it somewhere, you will lose marks. Be sure to put TanΘ = x somewhere before you begin to work out the equation using x as your variable.
x² + 5x + 6 = 0
With the equation in a more recognizable form, it may be easier to work it out. (I know it was for me!) The next step is to factor out the equation, so that you can find the values of x, and actual get the question done.
x² + 5x + 6 = 0
(x + 2)(x + 3) = 0
(TanΘ + 2)( TanΘ + 3) = 0
Since we finished factoring the equation, we can revert it back to its original form so that it is once again easier to work out. Due to the TanΘ being inside of a bracket, this question instantly becomes a breeze, and follows the exact same steps as the previous example.
TanΘ + 2 = 0 TanΘ + 3 = 0
TanΘ = -2 TanΘ = -3
calculator work
Tangentֿ¹(3) = Θr
Θr = 71.57
Now that we know our reference angle, the rest of the equation falls into place, by once again using CAST to find your quadrants, and going from there.
Quadrant II -> 180 - 71.57 = 108.43°
Quadrant IV ->360 - 71.57 = 288.43°
The final product from start to finish looks like the following.
Solve for Θ
Tan²Θ + 5tanΘ + 6 = 0
TanΘ = x
x² + 5x + 6 = 0
(x + 2)(x + 3) = 0
(TanΘ + 2)( TanΘ + 3) = 0
TanΘ + 2 = 0 TanΘ + 3 = 0
TanΘ = -2 TanΘ = -3
Calculator Work
Tangentֿ¹(3) = Θr
Θr = 71.57
Quadrant II -> 180 - 71.57 = 108.43°
Quadrant IV ->360 - 71.57 = 288.43°
Answer:TanΘ = 108.43°, 288.43°
That finishes off the lesson for today! For homework we have to complete the following Trigonometric Equations solving for theta.
2Sine²Θ - SineΘ - 1 = 0
5Sine²Θ + SineΘ - 2 = 0
These two questions are due tomorrow :)
3.) Notes/Things to Remember
- Remember CAST represents the trig functions that are POSITIVE in any given quadrant, and not the trig functions that are negative.
- Remember that if you are going to change TanΘ into x to mention it somewhere on the paper, preferably before any calculations. Failure to do this WILL result in a loss of marks.
- Remember to refer back to the reference angle when you are figuring out which Quadrant the answer should be in.
- When figuring out the value of Θr remember to use only the POSITIVE value. eg. TanΘ = -3, at this point you would use the positive value, which is 3 in this case. The reason for this is that you are trying the reference angle, which is always located in Quadrant I, which has all sine, cosine, and tangent values being positive.
__________________________________________________
That concludes my blog entry! wewt, I thought it'd never end. But thankfully it did, and now it's time for the moment you've all been waiting for. The time when you find out whom the next scriber will be. Guess what? Francis already knows who it is ;)
(For those of you who didn't understand, Francis is next =p )
Justus, over and out
Labels: Trigonometric Equations, Trigonometry
Trigonometry
What's the same?The shape of both graphs (a sinusoidal) is the same as well as the location of the zeroes.
What's different?The maximum and minimum has changed.
Amplitude: the height above or below the sinusoidal axis, which is the value in front of sine theta.
- If you're going to your terminal side from your initial side (counterclockwise), your angle is positive.
- Going the opposite direction (clockwise), will give you a negative angle.
Co-terminal: when two angles share the same side
Soo, that's my post. I'm so sorry it's not.. uhm.. great. I have a huuge headache right now and my sickness isn't getting any better. ^^;;
Anyways, on to the good part! Uhhmmm, the next scribe will be.. uhh.. Justus ?
Trigonometry: Graphs
Sigh... my turn to post. This is going to be about the whole graphing thing. Try not to get lost even though there's a good chance that you will. As you look and examine the images, you will see that there is some kind of pattern.You don't have to do sine for every single degree. Once you know all the angles in one quadrant, you can find any other angle in any other quadrant.
NOTE: Sine always the 'y' value. 
Unit CirclesThis helps you find the related angle.Cosine will always give and 'x' value and sine will always give you a 'y' value.eg. cos 30 degrees = 0.886 = the 'x' valuesin 30 degrees = 0.5 = the 'y' value
NOTES: The maximum value of a unit circle is 1 and the minimum is -1.
Every time you go around the circle, it's called a "period".Okay, this was a bad post and you know it. Once I started to do my post, I didn't really know what I was doing and that's not a good thing. SO... when I understand it better, i'll come back and edit this, tomorrow possibly.ANYWAYS... this part is the part that most people care about. Who's going to be the next scriber? JOSEPH... isn't the next scriber. Nelsa is! =D Have fun!
Trigonometry
Hey guys. My post will be about Trigonometry. oOo scared? Haha. Well sorry if this is kinda late :S
I will show you how to find the sine, cosine, tangent, and the angle theta when given a point.
You all should already know how to get the sine, cosine, and tangent, from grade 9 or 10 math.
Ex) Given a point at (6, 8) Find the sine, cosine, tangent, and the theta
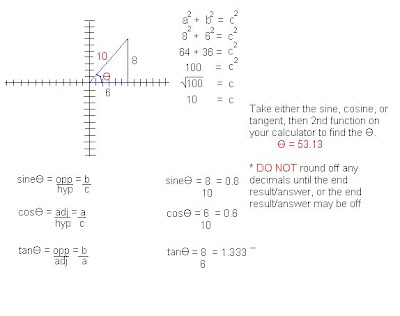
Be careful when finding sine, cosine, tangent and theta because it could be positive or negative, depending on the quadrant it is in.
A reference/related angle of a theta is in standard position. You would use the expression 180 -reference angle = theta.
Ex) If you are given an angle of 273 degrees, what is the reference angle?
NEVER give an answer for reference angle bigger than 90 degrees, only
ACUTE angles.
THE END :) .. hmmm who shall I choose for the next blog .. hmm I wonder who .. How about my good friend .. JASMIN .. hehehe Have fun Jasmin! Oh and don't forget, Ms. Ingram assigned Ex 8, #'s 1-3.
Labels: Unit Blog
does grammar count? nah this is mathwowquadratics was pretty okay, took some time understanding it at first but in the end it was a piece of cake, though my test tomorrow wont back up my overconfidence (lack of preparation), it's still a piece of cake. It's straight forward there's nothing that i shouldn't have understood. Twas a short lesson and i hope everything else is like this. Problem solving was "eh" some questions are simple and some require more work than others. The greatest part in quadratics was buying a calculator because it made me feel happy blowing 2 weeks of wages for a hand held device that doesn't even CONTAIN TETRIS! Graphing quadratics was as simple as pushing buttons. Not much to say anymore so I'm done. Cyaa
Pre-Test Blog
First of all, it was pretty easy and i thought i had it all, but i just realized i have much more to learn since we got the math dictionary, i realized how much i didn't know, and how much i had to memorize unless we got a formula sheet, unless the test will be easier than I thought. Other then that, the unit all together was pretty balanced, enough easy and enough hard work, balanced. I didn't think this unit would be easy, but yet I didn't think it would be this hard. Maybe i just found it hard because of all the extra homework I was getting, but that's just me. Until then BAI!
Unit Blog: Quadratic Functions
Alrighty... Quadratic Functions... In the beginning of this unit, Mrs. Ingram said that this stuff was suppose to be a review from last year, after she said that, I was freaked out at that moment because I didn't didn't know what the *bleep* she was talking about. I just went along with it for a while and I started to catch on. Now, this stuff is nothing to me! I can do it without a pencil! Okay, maybe not... but it's not as hard as I thought it would be. The best part out of this whole unit was using the graphing calculator. I'm not talking about the whole graphing part, I'm talking about writing little phrases on it. But if that doesn't count, then I would say that graphing the equations on the calculator was the best part. It makes things so much easier. The part I didn't really enjoy doing was the word problems. These word problems were just too confusing. Speaking of which, I must go and study that! - Jasmin
Blog Before The Test
Hi im richard. I think these unit was in the middle of hard and easy It was easy when you didnt have to complete the square with fractions. The fraction part is very dificult for me that is and allso the word problems that have to do with usually fences. well that is my take on this unit.
Pre-Test Blog for Quadratic Functions
Wow, this is my first blog! Haha.
Well, at the beginning of the semester, I thought this class was going to be difficult, and stressing, but now I think that it's not that bad, well not as bad as I expected. The first unit on Quadratic Functions was pretty good, it wasn't as hard as I imagined, but some parts like the fractions in completing the squares wasn't all that great. Haha
As I said up there ^^ the fractions in completing the squares wasn't all that great, but hey, not many people like fractions, like me. Haha
Well, I think that most of this unit was relatively easy, as long as I understood how to do the work, it was pretty simple.
So this is the end of my boring blog (I know that's what you're all thinking) Haha.
Goodluck to everyone on writing the test, and don't forget about the Math Dictionary tomorrow!
Pre-Test Blog
This is my blog prior to the test.
At first, I kind of had an overload in my head like I was reading another language, but after I got back into 'school mode', it started sinking in. Of course, I'm not gonna lie, I never like math but i do it anyways, so I have no positive feelings towards Quadratic Functions other than I learned something new.
It was difficult at first, but after a while, I found it not difficult, but extremely time consuming. Over time I learned what to do so it doesn't seem so hard, until there's some fractions throwin in just to mess with you. I also did not like dealing with word problems because they would sound very confusing at times, or maybe I was just confusing myself.
Did I think the unit was easy? No. Did I think the unit was hard? No. It's one of those in between things. Not hard, not easy, but gets to your head if your stuck on one question too long. The word problems proved to be annoying to me, as you had to arrange the right numbers in the right spots, or else your wrong. The graphing calculator proved very helpful, as you didn't necessarily have to do the work to find the vertex, max, min etc. The down side is that it's not the easiest thing to hold in your hand while doing work at the same time.
Test tomrrow ; Goodluck all.
Math dictionary due ; Once again, goodluck all =P
Mr.Lawrence ~ Out.
Unit Blog: Quadratic Functions
Okaay, so this unit was.. "ngeh". Hahha, honestly though, it's easier than most of the math stuff I had to learn before. It was "okay" in that it wasn't too difficult but I won't say it was easy either. I did think it would be harder, but well, you know, that's just me not having math for seven-ish months. ^^;;There wasn't anything I favoured above the others. But I did dislike the word problems (although it was relatively easier than others). What I did hate was having to learn how to use a new calculator. That threw me off and slowed the whole "learning" process, but I'm getting it. I'm going to miss my scientific calculator. *sniff*Overall I thought it was good. It was definitely a good way to start things off, it didn't require a whole lot of "intense" thinking (which is good because, hah, I was clueless when I walked into the classroom that first day).And.. yeah, that's it. XDD
My Thoughts
Overall, I thought that this unit was fairly simple. I didn't find anything too hard and at times, I found some questions easier than expected. It was also fun to learn how to graph my calculator since it makes things so much easier and it is also much faster. I also enjoyed completing the square, since I found it quite easy to understand. Of course I didn't like it when there were fractions involved, and I'm sure you guys also hate fractions XD. Anyways, the word problems weren't as bad as I thought they were, although I got confused with one question in the assignments we got.
Yeah..that's pretty much how I felt through this whole unit and I am not looking forward to the test =P. But oh well...I guess that's it. I'm going to go away now and finish my math dictionary >_<;. Ciao!
--Kristina
unit one: Quad. Functions
mhmm.. this unit wasn't as bad as i thought it was. at first i was just like 'whaaaat is this' sorta thing but it started to become easier i guess. lol i hated graphing without my graphing calculator so thank you for whoever invented this device (: hehe ohh and i know i'd probably sound like a bigger nerd but my favorite would have to be completing the square lol surprising, yes i know. though, i hate problem solving, they weren't so bad in this unit but i still dislike them as well as blogging. =/ but yeah anyways, this unit wasn't so stressing (: yaaayy oh yeah test tomorrow and dictionary thingy due.. ew haha kaayy byeeee and goodluck everyone :)-- roxanne yumang xoxo
Unit Blog: Quadratic Functions
Hiii everyone. Well, I think that this was one of those "okay" unit. It wasn't difficult for me and it wasn't easy neither. I liked graphing the equations on my graphing calculator. I hated completing the squares especially the fraction ones and the HARD word problems. yuuck. But, overall it was aallll goood. ohhh, blogging wasn't that BAD. SOOOO, bye and good luck on the test ! =D -RooooojuaneLabels: Unit Blog
THI'S TEST BLOG
OK here is my pre-test blog. Remember people, drink water before the test because your brain cannot function if it is not properly hydrated.
Anyway, as I was saying, this is my pre-test blog so I will give you my thoughts on the unit.
First of all, I would like to start by saying that this unit was relatively easy. The only thing I found difficult was completing a square when there were fractions in the equation. Besides that, graphing a parabola is super easy (especially if you have a graphing calculator.)
Although I found this unit simple, I couldn't say that I was fond of it.
That about wraps up my post. Peace out y'all!
Pre-Test Blog
This is my pre-test blog (As you may or may not have guessed by now) that we all have to do prior to the upcoming test, which will be happening on Tuesday, February 20th.In terms of how the unit was, I felt that it wasn't difficult, but required you to remember a whole bunch of little things, which turned out to be the hardest part of it. Everything else went smoothly however, and I am feeling somewhat confident about the test.The section of the unit that included Completing Squares turned out to be the hardest as I kept forgetting little things like to change the symbol (negative or positive) and such but eventually I began to get the hang of it.Overall I felt this unit was a good way to begin the semester, without being either too difficult, or too easy.~Justus
Blogging for Test
This is Paul (S.)'s pre-test blog entry #1 (my first ever entry :D)
> How do you feel about the unit?
Indifferent. About the same as anything else Ive ever learned in Math. Mild interest.
>Was there something you felt was difficult?
Not really. This unit felt pretty easy. Im sure that'll change though.
> Did you think the unit was easy?
Realitively.
So, this concludes my pre-test blog entry #1.
Edit: I couldn't figure out how to add my post to the rest. Sorry.
Labels: 1, one, Parabola, unit
Blogging for Test
Alright....This unit wasn't to difficult. At first we used a ToV (Table of Values) and sometimes I would end up getting one side of the parabola...so it looked like a linear equation, but I did figure out what I needed to do in the end to solve the question. Everything seemed straight forward. Vertex, AoS (Axis of Symmetry) Domain and Range, and the Intercepts. Perfect squaring wasn't that hard for me to do. I could do most of the word problems and the questions I couldn't do was becaues of the wording of the question.
I think that it was and good starting unit. We reviewed work for grade ten precal (in the exercises). Not to easy and not to difficult.
let’s do this! hmmm.... this is how i felt about this unit FUN! haha my friends who took math last sem was trying to explain this to me before but I was so confuse now I got it and I’m loving it =D
what I like most about this unit was completing the squares and finding the vertex and AoS I think that was easy for me and I actually enjoy them =D
I was having a hard time in word problems though hehe I never liked them. But the fact that there’s only 3 kinds of quadratic word problems, and that Ms.Ingram showed us examples of it makes it a little more easier for me=D and all the blog was very helpful too =D
anyways I really like this unit but I’m scared of the test =P
well good luck on the test everyone!
-paulette
quadratics!
hello, everyone_
This is how Ive felt while we are on quadratic functons_
Well, this was a lot different from just straight line graph_ which just takes form of y=ax+b
The shape of parabola was whoooooh_ so fresh_ o_oespcially that it can be open sidewards too, if the formula is ay²+by+c=x, was very interesting+_+the part I liked the best was _ word problems _ even three different kinds_because I learned SO MUCH about this quadratic function, im worried about my dictionary_i dont know how to put THAT much informationanyways I really enjoyed this unit_ but not the test plz ^-^
My Test Blog
I am creating this blog for the coming up test on Tuesday. On the to topic, the unit was quad-functions. During this unit, I did not find anything
particularly difficult. If you did not know, I have taken a part of this class before. This means I have had a peek into the unit. Overall, the unit was quite simple. I was able to do most of the work faster than other students without a calculator, not to brag.
" Quadratic Word Problems! "
SADst testing test asd testing teststst.
Hey guys, it's me, Elven. Sorry if the post took a while to get on, it took me a while to figure out how to log in, then when I did, I forgot my password -.- , blah blah, then I had to figure how to use this post thingy. Don't get fustrated! This is my first time posting! Sooo ...........
For Quadratic word problems, " THERE ARE 3 MAJOR TYPES OF PROBLEMS "
#1 - One thing will INCREASE while another thing will DECREASE
Example,Computer software sells for $20 each, 300 people will purchase at that price. For every 5 dollar increase, 30 fewer people will purchase. What is the maximum revenue? [ Trying to find vertex ]
[ Revenue - Price X number sold ]
Price --> 20 + 5x [ 20 is from the $20, +5 is the 5 dollar increase, and 'x' is the variable. It is going up. ]
Sold --> 300 - 30x [ 300 are the people, -30 is the fewer people purchasing, 'x' is the variable. It is going down. ]
and so... R = (20+5x)(300-30x)
= 6000 - 600x + 1500x - 150x²
= 600 + 900x - 150x² [ And now you have to rewrite this in the x2 + x + # so it is factorable ]
= -150x² + 900x + 600 [ Now you want to complete the square, *Negative coefficient = going downwards. ]
= -150(x² - 6x + _____ ) + 6000 [ Factored out 150, now to find 3rd term, divide mid. term by 2, then square ]
( 6/2 = 3² = 9 )
= -150(x² - 6x + __9__ ) + 6000 [ What you really put in the brackets was -150(9) = -1350 so to keep it balanced on the outside of brackets, you add 1350 ]
= -150(x² - 6x + __9__ ) + 6000 + 1350 [ Now you have to convert it to a(x-h)² + k ]
= -150(x-3)² + 7350 [ Now that you know the variable, you'd want to plug in the information ]
20 + 5(3) = 35
300 - 30(3) = 210
.. (35)(210) = 7350
*If you go back and check the y vertex, it is the same as the answer. o0o lala.
#2 - Ussually (always) you are finding a maximum area based on a linear amount of fencing, string, rope. [ Basically anything that is enclosing ]
Example,
What is the maximum rectangular area that can be enclosed by 120m of fencing, if one side of the rectangle is an existing wall?
-- ** ~~ !!!HINT OMG!!! ~~ ** -- .... DRAW A DIAGRAM ....
Here is my beautiful diagram
ok as you can see, i named the left and right side " W " and " L " is
the bottom side, Which is ..
120m subtracted by the 2 sides, which is W .. [ Trying to find vertex ]
To find the area ... [ A = lXw ]
So (120-2w)(W)
= 120w-2w² [ Rewrite, just as I did above ]
= -2w² + 120w [ Factor and complete the square]
= -2(w² - 60w + _____ ) + 0 [ Mid. term divided by 2, then squared ]
( 60/2 = 30² = 900 )
= -2(w² - 60w + __900__ ) + 1800 [ Actually added -1800 in the brackets, so balancing out you add 1800 outside brackets. Now you convert to a(x-h)² + k ]
= -2(w-30)² + 1800
[ Vertex = (30, 1800) ]
Now to plug in the information ...
W = 30
L = 120 - 2(30) = 60
(30)(60) = 1800
*Wow! Once again equaling the y vertex. MIND BLOGGLING!!
#3 - [ GIVEN AN EQUATION ]
Ussually something shot inro the air or dropped from a height.
Example,
A projectile is shot straight up from a height of 6m with initial velocity of 80m/s. It's height is given by the equation.
h = 6 + 80 - 5t² [ If you're spending time wondering where the 5 came from, the equation was given along with the question .. Like the title says ' GIVEN AN EQUATION ' ]
After how many seconds will it reach it's maximum height? What is that height? [ Eaazzzy pweeezzy, we got the equation so .. ]
H = 6 + 80 - 5t² [ Now you ' rewrite the sucker ' words of Ingram ]
H = -5t² + 80t + 6 [ Facter and complete square ]
= -5(t² -16t + _____ ) + 6
( -16/2 = (-8)² = 64 )
= -5(t² - 16 + __64__ ) + 6 + 320 [ Balancing outside and inside brackets. Then convert to a(x-h)² + K ]
= -5(t-8)² + 326
So the time it will take to reach the maximum height is 8 seconds [ X point of vertex ]
And the maximum height is 326m [ Y point of vertex ]
I'm DONE! YES! I think thats all.. Whew. Thanks for reading .. if you did -.- ... Oh man im hungry! I'm out.
Oh yeah, almost forgot. Next poster or whatever you guys call it will be swan. I mean Xuan Bwhahahaha!!! x)
P.S. Correct any mistakes for me please and thanks.
Labels: Testing
Factoring -_-
hiiii.. helloo fellow peers as you all know i am roxanne and unfortunately i'm the next scriber (thumbs down)today's class we learned how to factor perfect squares
REVIEW:
1. X²+2x+1 = (x+1)²
2. X²-2x+1 = (x-1)²
3. X²+4x+4 = (X+2)²
4. X²-4x+4 = (X-2)²
as you can see there is a pattern which is to divide the middle term by 2 then square it to get the final term of the equation
example.
X²+6X+9 --> middle term is 6x therefore you must divide it by 2 which will equal to 3. second step is to square it, which will then equal 9
REMEMBER: final term is always positive
COMPLETING A SQUARE
the equation will look like this:
y = ax²+bx+c but must be converted to y = a(x-h)²+k form
- to complete this, you must find the middle term, divide by 2, then square it
- just like the pervious questions above
example ONE.
y = x²+4x-5 convert into a(x-h)²+k form
1st step: rewrite question to y = x²+4x+ _____ -5
2nd step: find the final term by dividing the second term (4) by 2 then squaring it.
4/2 = 2² --> 4
y = x²+4x+ __4___ -5 -4REMEMBER: what you do on one side you must do to the other side therefore you must subtract 4 on the other side.
3rd step: factor x²+4x+4 then solve the other part of the equation which is -5-4
final answer: (x+2)²-9
now you can find the:vertex: (-2, -9) ---> (h,k)A0S: x = -2Domain = (-00, 00)Range = [-9, 00)
example TWO
when there is a coefficent infront of the X² you must factor it out.
y = 3x²-12x+16
1st step: rewrite to 3x²-12x ____ +16
factor out the 3 so it will look like this
3(x²-4x+____ ) +16
2nd step: find the final term by dividing the second term (-4) by 2 then squaring it
-4/2 = (-2)² --> 4
3(x²-4x+__4__ ) +16-12REMEMBER: what you do on one side you must do to the other sidesince you're multiplying 3 by everything in the brackets, you must multiply 3 by 4 which gives you 12therefore you must SUBTRACT 12 from 163rd step: factor what is in the brackets (x²-4x+4) then solve 16-12final answer: 3(x-2)²+4vertex: (2, 4)AOS: x = 2Domain: (-00, 00)Range: [4, 00)example THREE
When dealing with FRACTIONS, use the same steps to find the answery = -2x²-5x+31st step: factor out the -2, since you cannot factor -2 from 5 you must put it into fraction form (5/2)-2(x²+5/2 _____ ) +32nd step: find final term by dividing 5/2 by 2 then squaring it. 5/2 x 1/2 = (5/4)(5/4) -->
25/16
-2(x+5/2+ __25/16___ )+3+50/16 -
2(x+5/2+ ___25/16__ ) +3+ 25/8 (reduced)REMEMBER: what you do on one side you must do to the other and since you're multiplying everything in the brackets by 2 you must multiply 25/16 by -2 then ADD it to the +33rd step: factor what is in the brackets which will give you -2(x+5/4)² +24/8+ 25/8 (the 5/4 came from what you figured out when you multiplied 5/2 by 1/2)final answer: -2(x+5/4)x²+49/8vertex: (-5/4, 49/8)AOS: x = -5/4Domain: (-00, 00)Range: [-00, 49/8)woott i'm done (: well i'm pretty sure i'm done lol if there are any mistakess please edit LOL hahaaa i hope i did this right. kaaay anywayss NEXT SCRIBER WILLL BEEEEE ELVENN! MUAHAHAHA
Quadratic Functions [Cont'd]
Greetings, I, Mr.Lawrence, am today's scribe.
Review; In general, y = ax² or x = ay² [Negative 'a' value will open the x = ay² function to the left.]
So, If a > 0 parabola opens upward ( x² )
If a > 0 parabola opens right ( y² )
Therefore, If a < 0 parabola opens downward ( x² )
If a < 0 parabola opens left (y²)
You should recognize a > 1 ; the parabola will be narrower ( skinnier )
*Note: a represents an absolute value
a < 1 ; the parabola will be wider.
The following parabolas are:
y = x² ; Vertex (0,0) AOS ; X = 0 Domain ( -00, 00) Range [0,00)
y = x² + 3 ; Vertex (0,3) AOS ; X = 0 Domain (-00,00) Range [3,00]
y = x² - 5 ; Vertex (0,-5) AOS ; X = 0 Domain (-00,00) Range [-5,00)
As we can see, there is a relationship.
Equation in the form of y = ax² + k
- The K Value directs/shifts the graph vertically.
-> If "K" is positive, Graph goes up
-> If "K" is negative, Graph goes down
AOS of all graphs is X = 0
The vertex is (0, K) so we know right away, what the vertex is just by looking at the equation.
Now the next equation is y = (x+1) ² and y = (x-1)²
This equation is in the form of y = (x-h) ² "h" is affecting the graph, shifting it horizontally.
*Note:
1) Axis of semmetry is the line x = h
2)Coordinates of vertex are (h,0)
3)If "h"> 0 parabola shifts to the right (x - h)
If "h"< 0 parabola shifts to the left ( x + h )
So, giiven y = (x-3)² +4 [which is basically, y= a(x-h) + k] the vertex would be (h,k) and because we know what "h" and "k" are 3, and 4, already we know the vertex is (3,4)
Domain = (-00,00) Range [4,00) <- The range is different for this equation. Axis of symmetry is x = h. Given y = -(x-1)² = 4
Vertex; (1,4)
AOS ; x =1
Domain ; (-00,00)
Range(-00, 4]
Direction of opening ; Downward
How to find Zeroes ;
First we factor out
y = -(x-1)(x-1)+4
Multiply the polynomials
= -(x²-2x+1) +4
Use the negative sign to change the sign
= -x²+2x-1+4
Put 0
in place of y because we're finding the zeroes.
0 = -x² +2x+3
Factor out the negative
0 = -(x²-2x-3)
Factor more
0 = - (x-3)(x-1)
Therefore x = 3, x =1, Existing zeroes are 3,1.
That's it.
Next scribe will be... duck, duck,
Roxee.
DAY 2: QUADRATIC FUNCTIONS
Graphing it looks like:
The general form of y=x2 is y=ax2
The a (coefficient) in the equation can be any value.
The next question on the board was: y=2x2
Once again you need to make a table of values.
Graphing it looks like:
NOTE:
* When the coefficient "a" is greater than 1:
-parabola will stretch vertically
-can compress horizontally
- either way it will look narrower than x2 graph
* Coefficient is greater than 0 but less than 1:
-parabola will stretch horizontally
-it is a wider graph than x2
Eg. y=1/2x2
* If the coefficient is negative, the graph opens downward:
Eg. y=-x2
* Whenever the coefficient is positive the graph opens to the right of the x-axis and the negative coefficient goes the opposite direction:
Eg. right: x=y2 and left: x=-y2
This wraps up today's lesson on Quadratic Functions.
I hope this is helpful and don't forget to do your homework:
Exercise #2 questions: 2-5 AND Exercise #3 questions: 1-3
Next SCRIBE: Mr. Lawrence, I choose you! (poke ball prop) Have fun! =D
Farewell friends, see you in class! Labels: scribe post
Parabola
Vertex - Minium / or max point on a parabola
Axis of semetry always goes through the vertex
When doing interval notation
solid circle - the value is included
- So use a Square bracket
Open Circle-The value is not included
- So use a Round bracket
X-intercept, Zeros and Roots of equation are all the same thing just different way of asking for them
Next scribe will be Rojuane
Labels: Parabola
Welcome!!
Welcome to your class blog.
This blog is intended to help you help each other as we work through the Grade 11 Pre-calculus course. I hope you make good use of this tool and enjoy the course. Good luck with the course.
Mrs. Ingram
Pretty scary ain't it? Well, nothing is missing as though it may look..bmp)
SinB = 1.23(since its impossible to have a sine value of >1. Can't find angle B. Therefore it's no triangle!
Now to form 1 triangle. Sine Law comes into play...now.2.bmp)
In Quad I H = 56.44°
g = 11.98 cm(the first g side)
g(2) = 5.34 cm(2nd g side)
