Solving Trig Functions (for dummies)
Alright, since Nelsa decided to unleash the evil that is scribe unto me, I shall be scribing about the lesson given February 26th, 2007 (For those of you bad people whom may or may not have been there.)Synopsis: The lesson here was comprised mostly of how to solve trigonometric equations (Equations that use Sine, Sosine, or Tangent, in place of x or other variables). We briefly covered the related angles of 30°, 45°, and 60° on the coordinate circle that Cosine, Sine, are derived from, and how those sine, cosine, and tangent measurements can be used to solve triangles/trigonometric equations. We also reviewed the use of CAST, as an effective tool for remembering which trigonometric functions are negative in which quadrants.
Table of Contents
1.) Coordinate Circle
- Sine, Cosine, Tangent Values of 30° , 45° , and 60°
- Sine, Cosine, Tangent Values of related angles found in the II, III, and IV quadrants
2.) Intro to Trigonometric Equations
- Basics
- Variations/How to solve them
- Finding the Quadrant
3.) Conclusion/Afterword to Trigonometric Equations
- Notes/Things to remember
*Note* Before I get into it, I'd like to mention that if you should find any mistakes with what I've written, feel free to tell me, or change it yourself. I'm not a expert on this and I do make mistakes, so just change it if it's wrong :p Anyways, down the rabbit hole we go, into the world of ridiculous mathmatics*
1.) Coordinate Circle
Well I'm sure we're all familiar with that lovely circle that the Trig functions, Sine, Cosine, are derived from, the one with the Domain ( -1, 1) and range of (-1, 1). Anyways, in addition to the measures of 30° , and 60° , we found the cosine, sine, and tangent values for 45° which can be seen on the following diagram.
Red Background = Quadrant I
Yellow Background = Quadrant II (Note, I am aware that this is orange, but yellow wouldn't show up on the white background, so don't bug me about it ^.^ )
Green Background = Quadrant III
Blue Background = Quadrant IV
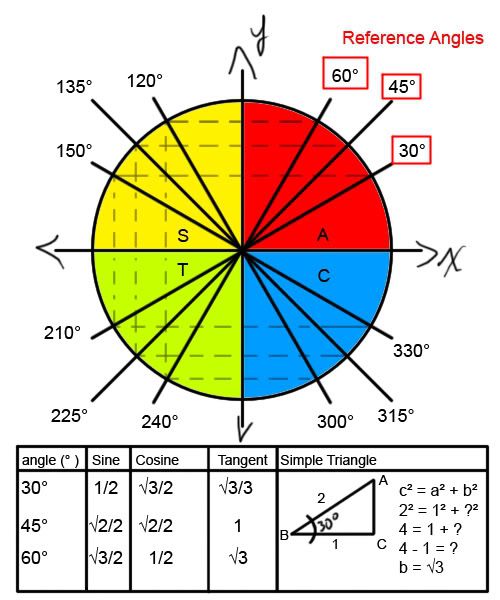
*Note* The triangle in the image is a Right angled triangle
Now, you may be wondering, how we found out the values of these angles, at said degrees, and it is with this question in the air, that I introduce you to the simple Right Angled Triangle that our splendid teacher, Mrs. Ingram drew up for us. This triangle has been illustrated on the bottom of the coordinate circle chart I made up. All the math for the simple triangle is included, and should be easy to follow. We started with two sides (The hypotenuse which was 2, and one leg, which was 1.) and using the pythagorean theorum, came up with an exact value of √3 for the final leg. From there determining the values of Sine, Cosine, and Tangent, at each angle (30, 60, and 45 degrees) was simply a matter of using SOH, CAH, TOA. The values of these can be found in the other half of the table where the simple triangle is found. Now finding the values of each related angle in every quadrant was simply a matter of using CAST.
*Note* Due to the fact that Sine = y, Cosine = x, and Tangent = y/x quadrant I's sine, cosine, and tangent values are positive. In Quadrant II Sine is positive, while Cosine and Tangent are Negative. In Quadrant III, Tangent is positive (because -sine/-cosine = a positive value), while Sine and Cosine are negative. Finally in Quadrant IV Cosine is positive, while Sine and Tangent values are negative.
The values of the remaining angles are as follows.
120° ----> Sine = √3/2 Cosine = -1/2 Tangent = - √3
135° ----> Sine = √2/2 Cosine = -√2/2 Tangent = -1 } ---- Quadrant II Angles
150° ----> Sine = 1/2 Cosine = -√3/2 Tangent = √3/3
210° ----> Sine = -1/2 Cosine = -√3/2 Tangent = √3/3
225° ----> Sine = -√2/2 Cosine = -√2/2 Tangent = 1 } ---- Quadrant III Angles
240° ----> Sine = -√3/2 Cosine = -1/2 Tangent = √3
300° ----> Sine = -√3/2 Cosine = 1/2 Tangent = -√3
315° ----> Sine = -√2/2 Cosine = √2/2 Tangent = -1 } ---- Quadrant IV Angles
330° ----> Sine = -1/2 Cosine = √3/2 Tangent = -√3/3
And that sums up this section of the blog (whew ^.^)
2.) Intro to Trigonometric Equations
Now that we're past the Coordinate Circle recap, it's time to move onto the main portion of the lesson. Trigonometric Equations. Trig equations aren't much different for any other equation with the exception of the fact that when solving you have to deal with the form:
0 ≤ Θ ≤ 360°
To begin we'll look at a generic equation
Solve for x
2x - 1 = 0
2x/2 = 1/2
x = 1/2
To solve this equation is no feat. You simply divide out the coefficient of the variable, and move the -1, over to the other side of the = symbol, inverting the symbol as you go.
Now, we're going to apply this to a trigonometric equation.
Solve for Θ
2SineΘ - 1 = 0
2SineΘ/2 = 1/2
SineΘ = 1/2
To do this we could follow the exact same procedure, with the exception that at the end of it all, there are a few more steps to do, because of the fact that we're dealing with degrees. So once you've gotten to the final step shown above, you still need to find the value(s) of theta. To do this you simply input the Sine inverse of whatever sine theta equals while positive into your calculator.
Sineֿ¹(1/2) = 30°
Whatever value comes out of this calculation is now your Reference angle, and can be used to find the related angles, thus finishing the question. Because the value of Sine theta was a positive value, you know that the related angle can be, only in Quadrant II (You know this because of CAST. In quadrant II Sine values are positive. You already have the Quadrant I value, which is your Reference angle.) So now the finished equation looks like this.
Solve for Θ
2SineΘ - 1 = 0
2SineΘ/2 = 1/2
SineΘ = 1/2
Θ = 30°
Θ = 180 - 30° = 150°
Now that you've seen the basics of a trig equation, it's time to see the variations you can have.
Solve for Θ
Tan²Θ + 5tanΘ + 6 = 0
Before you start to tackle a question like this you may want to convert it into a more recognizable format.
*Note* If you convert the variable of an equation without stating it somewhere, you will lose marks. Be sure to put TanΘ = x somewhere before you begin to work out the equation using x as your variable.
x² + 5x + 6 = 0
With the equation in a more recognizable form, it may be easier to work it out. (I know it was for me!) The next step is to factor out the equation, so that you can find the values of x, and actual get the question done.
x² + 5x + 6 = 0
(x + 2)(x + 3) = 0
(TanΘ + 2)( TanΘ + 3) = 0
Since we finished factoring the equation, we can revert it back to its original form so that it is once again easier to work out. Due to the TanΘ being inside of a bracket, this question instantly becomes a breeze, and follows the exact same steps as the previous example.
TanΘ + 2 = 0 TanΘ + 3 = 0
TanΘ = -2 TanΘ = -3
calculator work
Tangentֿ¹(3) = Θr
Θr = 71.57
Now that we know our reference angle, the rest of the equation falls into place, by once again using CAST to find your quadrants, and going from there.
Quadrant II -> 180 - 71.57 = 108.43°
Quadrant IV ->360 - 71.57 = 288.43°
The final product from start to finish looks like the following.
Solve for Θ
Tan²Θ + 5tanΘ + 6 = 0
TanΘ = x
x² + 5x + 6 = 0
(x + 2)(x + 3) = 0
(TanΘ + 2)( TanΘ + 3) = 0
TanΘ + 2 = 0 TanΘ + 3 = 0
TanΘ = -2 TanΘ = -3
Calculator Work
Tangentֿ¹(3) = Θr
Θr = 71.57
Quadrant II -> 180 - 71.57 = 108.43°
Quadrant IV ->360 - 71.57 = 288.43°
Answer:TanΘ = 108.43°, 288.43°
That finishes off the lesson for today! For homework we have to complete the following Trigonometric Equations solving for theta.
2Sine²Θ - SineΘ - 1 = 0
5Sine²Θ + SineΘ - 2 = 0
These two questions are due tomorrow :)
3.) Notes/Things to Remember
- Remember CAST represents the trig functions that are POSITIVE in any given quadrant, and not the trig functions that are negative.
- Remember that if you are going to change TanΘ into x to mention it somewhere on the paper, preferably before any calculations. Failure to do this WILL result in a loss of marks.
- Remember to refer back to the reference angle when you are figuring out which Quadrant the answer should be in.
- When figuring out the value of Θr remember to use only the POSITIVE value. eg. TanΘ = -3, at this point you would use the positive value, which is 3 in this case. The reason for this is that you are trying the reference angle, which is always located in Quadrant I, which has all sine, cosine, and tangent values being positive.
__________________________________________________
That concludes my blog entry! wewt, I thought it'd never end. But thankfully it did, and now it's time for the moment you've all been waiting for. The time when you find out whom the next scriber will be. Guess what? Francis already knows who it is ;)
(For those of you who didn't understand, Francis is next =p )
Justus, over and out
Labels: Trigonometric Equations, Trigonometry

0 Comments:
Post a Comment
<< Home