Grade 11 Pre-Cal E

Central and Inscribed Angles

Alrighty, well roxee picked me to do the blog for today, so that would explain why I'm posting. Anyways for those of you who might not have been in class today (the 9th of May) we did some more work with circles and chords, specifically finding out about Central angles, and Inscribed angles. So, without further adeu, on with the blog!

Inscribed and Central Angles

A few quick definitions and points about Inscribed angles, Central angles, and the word subtended. (*Note* These make up the majority of todays lesson, so it would be good to read this if you weren't present.)

Central Angle - The vertex the central angle is at the center of the circle, and is equivalent to twice the inscribed angle.

Inscribed Angle - The vertex of an inscribed angle is located on the circumference of the circle.
- If the endpoints of two inscribed angles are the same, the measurement of those angles is also the same.
- Inscribed angles that are subtended by the same arc have the same measure.
- Inscribed angles are half of the central angle.

Subtended - The point at which an arc 'cuts' an angle, ending the angles. Example. Arc AB subtends Angle ADB at points A and B (because the lines making up angle ADB technically go on forever, they are considered "subtended" by arc AB, as they do not continue past the arc.)

Now, with those three points out of the way we have our nifty little diagram that I threw together. Now it isn't perfectly drawn up, so the center may not be at the exact center, and the angles may not be exactly 90 degrees, but for the sake of my sanity, we will assume they are, as they would be if everything was done perfectly.



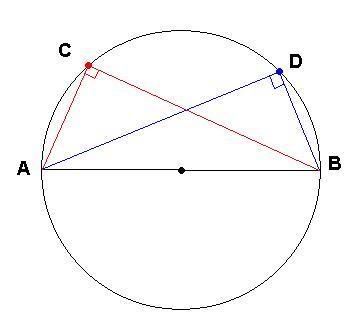
So, on the graph you'll notice a line, that is the diameter of the circle. This line is labeled AB. There are also, two angles, ADB, and ACB, both of which are designated as 90 degree angles. Both of these angles are inscribed angles, and were made by picking some point on the circumference of the circle, and joining it to the endpoints of the diameter of the circle (A and B).

Now you may be wondering the use of this, and the answer is simple. Since you are constructing right angled triangles that happen to have the diameter of your circle as one of their sides, you can use these inscribed angles to find various thing out about your circle. These things include, obviously, the diamter, the radius, and many things I'm sure we will learn about tomorrow in class ;p

So for those of you who missed it. The homework for today is Exercise 30, questions 9, 10, 12, and 14. AND Exercise 31, questions 1 to 3. :)

Anyways I'm pretty sure that that sums up todays lesson. Nothing too huge, as we always expect to see at the beginning of a unit. If I missed anything, or didn't explain something well feel free to scold me and say your right and I'm not :P I'll be sure to change it asap.

So! Now comes the best part of the blog. Picking the next blogger!! >D I think I'mma go with my projectmate, the lovely Xuan. Have fun! ;)

Now it's off to work for me -_-;

posted by Skyline @ 4:29 PM