Blog Entry #51 (The 3rd way to find the roots)
Hello, and welcome one and all...Since someone decided to elect me as the scribe, I must now write a post on the topic covered today in Maths class (Today being March 12th, 2007). I hope you find this post informative and helpful :D
---------------------------------------------------------------------------------
Mini-Legend: I use some characters that are can only be properly viewed with one of the "basic" fonts (eg. Times New Roman, Arial).
These include:
└> (an L symbol with an arrow) - This just means that this goes from the step above to the step being pointed to (>)
√ - This is supposed to be the square root sign I think.
+/- - This means that the result can be positive or negative
+/-√ - An combination of the previous entries. This means that the resultant root will either be positive or negative.
--------------------------------------------------------------------------------
Our topic today was: The 3rd way to find the roots/zeros of a parabola
In simple terms, we will use Square roots to find the roots of a parabola. Coincidence? I think not!
> First, we shall simply solve for the square, like usual:
>> x² + 8x + 7 = 0
└> (x² + 8x + ___) + 7 = 0
└> (x² + 8x + 16) + 7 - 16 = 0
└> (x + 4)² - 9 = 0
> But this is where things turn to THE TWILIGHT ZONE!
> We will now boggle your mind!
>> (x+4)² = 9
> We have now moved the 9 over to the other side of the =. Now, we will solve for x!
> But to do that, we must get rid of that pesky ². So we square root both sides!
>> x + 4 = +/-√9
> (Heres what it would look like were you writing it out on a pencil or paper)
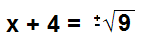
> Now we're almost done!
>> x = -4 +/-√9
> But here comes the tricky part!
> Because the square root of 9 can be + OR -, we get two different outcomes (which means two different values of x). So we have to find the x value for both (which gives us the roots!)
>>> x = -4 + 3
└> x = -1
> OR
>>> x = -4 - 3
└> x = -7
> SO WE CAN DEDUCE....
>> x = -7, -1
> Dont forget to put them in coordinate form:
>> (-7, 0) (-1, 0)
> IF YOU'RE IN DOUBT, CHECK WITH YOUR GRAPHING CALCULATOR!
> Like so...
The equation...

And the intercepts!

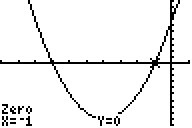
> And that my good fellows, is how you use Square roots to find the roots of a parabola.
> Mind you, the number on the outside will not always be a number with a whole square root. Sometimes the darn thing will have to be left as a square root, in which case you'd just leave your answer as something like this:
>> x = -4 -√9, -4 + √9
>> x = (-4 - √9, 0) (-4 + √9, 0)
> This is also acceptable, but only when it cannot be further simplified.
> But now we must progress into another level of equation, and solve those!
>> 3x² + 12x + 21 = 0
> That evil fiend, coefficient has siezed the x²! Lets get em!
>> x² + 4x + 7 = 0
> Take that! This time, we wont simply put the 3 outside as a coefficient again, we have to eradicate him completely!
> Now we can proceed in peace!
>> (x² + 4x + ___) + 7 = 0
└> (x² + 4x + 4) + 7 - 4 = 0
└> (x + 2)² + 3 = 0
└> (x + 2)² = 3
└> x + 2 = +/-√3
└> x = -2 +/-√3
> So, we just do the usual...
>>> x = -2 +√3
>>> x = -2 -√3
>> x = (-2 +√3, 0) (-2-√3, 0)
> There is one final variation to the equation that we must deal with! It is the evil, almighty fraction!
>> 1/2x² + 3/2x = - 3/5
> But we have our secret weapon. Multiplication power!
>> 2(1/2x² + 3/2x + 3/5) = 2(0)
└> x² + 3x + 6/5 = 0
>There may be some leftover fraction, but do not despair! We can still prevail!
>> (x² + 3x + ___) + 6/5 = 0
└> (x² + 3x + 9/4) + 6/5 - 9/4 = 0
> Just find a common denominator!
>> (x + 3/2)² + 24/20 - 45/20 = 0
└> (x+3/2)² -21/20 = 0
└> (x+3/2)² = 21/20
└> x+3/2 = +/-√21/20
└> x = -3/2 +/-√21/20
> And a final step...
>>> x = -3/2 + √21/20
>>> x = -3/2 - √21/20
>> x = (-3/2 - √21/20, 0) (-3/2 + √21/20, 0)
> For purposes of checking my answers, I will decimalize the answers and use my graphing calculator to check them.
The decibalization (is that a word? [Spellcheck doesnt think so ):])


The equation.

The results are in!


And that is all! Cheers to finishing my first ever scribe entry!
--------------------------------------------------------------------------
Now we can all find out who the next scribe is!
(If you can't guess this one, well...)
I pick mhi.
I mean Thi.
--------------------------------------------------------------------------
I would also like to recommend that if one wishes to show something from their graphing calculator, they might want to use the TI Connect ScreenCapture tool. Its much easier to read and faster than a webcam I think ;D
--------------------------------------------------------------------------
Feel free to point out any mistakes I may have made, I will try to correct them quickly.
Special Thanks to:
Francis
Character Map
The Internet
Paint (the program)
TI Connect ScreenCapture Tool
Special Unthanks to:
Whoever made this writing window so small.
Seriously, it takes like a whole minute to get the picture in the right spot, and it feels so cramped ):
This scribe post took approximately 2 hours to complete.
That's all, folks!

0 Comments:
Post a Comment
<< Home